ソートは、検索可能性を高めるために配列の要素を特定の順序で配置する基本操作です。 簡単に言うと、データは簡単に検索できるようにソートされています。
比較表
| 比較基準 | 挿入ソート | 選択ソート |
|---|---|---|
| 基本 | データは既存のソート済みファイルにデータを挿入することによってソートされます。 | データは、連続した要素を選択してソート位置に配置することによってソートされます。 |
| 自然 | 安定している | 不安定 |
| 従うべきプロセス | 配置する場所は検索されますが、要素は事前にわかっています。 | 要素が検索されている間、場所は以前からわかっています。 |
| 即時データ | 挿入ソートは、即時データを処理できるライブソート技法です。 | それは即時データを扱うことができません、それは始めに存在する必要があります。 |
| ベストケースの複雑さ | に) | O(n 2 ) |
挿入ソートの定義
挿入ソートは、既存のソート済みファイルに一連の値を挿入することによって機能します。 一度に1つの要素を挿入することによってソートされた配列を構築します。 このプロセスは、配列全体が何らかの順序でソートされるまで続きます。 挿入ソートの背後にある主な概念は、各項目を最終リストの適切な場所に挿入することです。 挿入ソート方法は、有効な量のメモリーを節約します。
挿入ソートの働き
- 一方はソートされたデータを格納し、もう一方はソートされていないデータを格納する2セットの配列を使用します。
- ソートアルゴリズムは、ソートされていないセットに要素が存在するまで機能します。
- 配列に 'n'個の要素があるとしましょう。 最初は、インデックス0(LB = 0)の要素がソートセットに存在します。 残りの要素はリストのソートされていないパーティションにあります。
- ソートされていない部分の最初の要素の配列インデックスは1です(LB = 0の場合)。
- 各反復の後、ソートされていないパーティションの最初の要素を選択し、それをソートセットの適切な場所に挿入します。
挿入ソートの利点
- 小さなデータセットで使用すると簡単に実装でき、非常に効率的です。
- 挿入ソートの追加のメモリスペース要件はより少ない(すなわち、O(1))。
- 新しい要素が受け取られたときにリストをソートすることができるので、ライブソート技術であると考えられています。
- 他のソートアルゴリズムよりも高速です。
例:
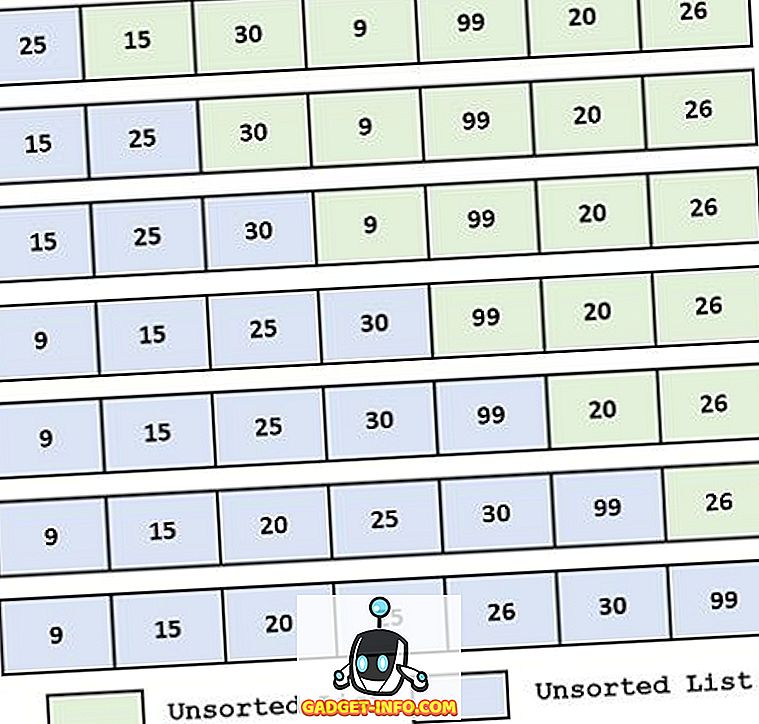
選択ソートの定義
選択ソートでは、最小値の番号を検索し、それを順序に従って昇順または降順に並べ替えます。 最小キーを検索して適切な位置に配置するプロセスは、すべての要素が正しい位置に配置されるまで続けられます。
選択ソートの働き
- メモリ内にN個の要素を持つ配列ARRを仮定します。
- 最初のパスでは、最小のキーがその位置とともに検索され、次にARR [POS]がARR [0]と交換されます。 したがって、ARR [0]はソートされます。
- 2回目のパスでも、最小値の位置がN − 1個の要素のサブアレイ内で決定される。 ARR [POS]をARR [1]と交換します。
- パスN − 1では、N個の要素をソートするために同じプロセスが実行される。
例:
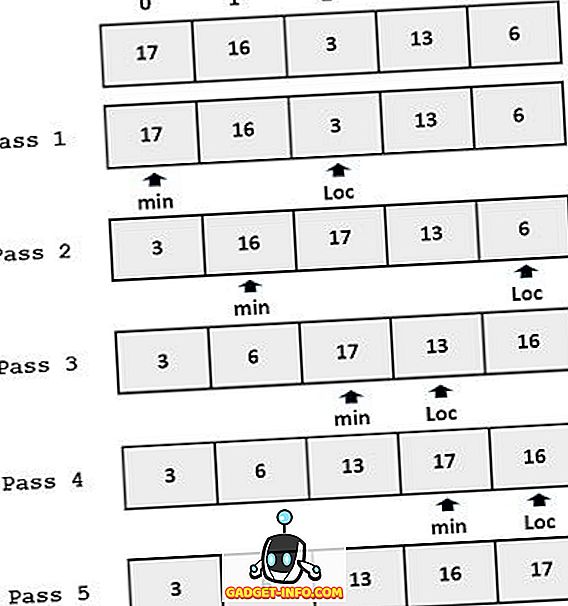
挿入ソートと選択ソートの主な違い
- 挿入ソートは通常挿入操作を実行します。 反対に、選択ソートは必要な要素の選択と配置を実行します。
- 選択ソートは安定したアルゴリズムではありませんが、挿入ソートは安定していると言われています。
- 挿入ソートアルゴリズムでは、要素は以前から知られています。 対照的に、選択ソートは事前に位置を含みます。
- 挿入ソートはライブソート技法で、到着した要素はリスト内で即座にソートされますが、選択ソートは即時データではうまく機能しません。
- 挿入ソートは、最良の場合、実行時間がO(n)です。 それとは対照的に、選択ソートの実行時の最良の複雑さはO(n 2)です。
挿入ソートの複雑さ
挿入ソートの最も複雑なケースは、 O(n)回です。つまり、配列が以前にソートされている場合です。 同様に、配列が逆の順序でソートされると、ソートされていない配列の最初の要素がソートセットの各要素と比較されます。 したがって、最悪の場合、挿入ソートの実行時間は2次、つまりO(n 2)になります。 平均的な場合にも、それは最小の(k-1)/ 2の比較をしなければなりません。 したがって、平均的な場合も2次実行時間O(n 2)を持ちます。
選択ソートの複雑さ
選択の働きとして、並べ替えは配列内の元の要素の順序に依存しないため、選択並べ替えのベストケースとワーストケースの複雑さに大きな違いはありません。
選択ソートでは、最小値の要素が選択されます。選択プロセスでは、すべての 'n'個の要素がスキャンされます。 したがって、n-1回の比較は最初のパスで行われます。 そして、要素は交換されます。 同様に2回目のパスでも、2番目に小さい要素を見つけるために、残りのn − 1個の要素を走査する必要があり、プロセスはアレイ全体がソートされるまで続けられる。
したがって、選択ソートの実行時間の複雑さはO(n 2)です。
=(n-1)+(n-2)+……….. + 2 + 1
= n(n-1)/ 2 = O(n2)
結論
両方のソートアルゴリズムのうち、挿入ソートは高速、効率的、安定的ですが、選択ソートは少数の要素が含まれる場合、またはリストの一部が以前にソートされている場合にのみ効率的に機能します。 選択ソートによって行われた比較の数は実行された移動よりも多いのに対し、挿入ソートでは要素が移動または交換された回数は行われた比較よりも多い。