これとは対照的に、 組み合わせの場合、順序はまったく問題になりません。 数学だけでなく実際の生活においても、私たちはこれら二つの概念を定期的に経験しています。 しかし、私たちはそれに気付くことはありません。 したがって、この2つの概念がどのように異なるのかを知るために、この記事を注意深く読んでください。
比較表
| 比較基準 | 順列 | 組み合わせ |
|---|---|---|
| 意味 | 順列とは、オブジェクトのセットを順番に並べ替えるさまざまな方法のことです。 | 組み合わせとは、オブジェクトの順序が問題にならないように、多数のオブジェクトから項目を選択するためのいくつかの方法を指します。 |
| 注文 | 関連する | 無関係 |
| を意味します | 配置 | 選択 |
| それは何ですか? | 順序付けされた要素 | 順不同セット |
| 答え | 与えられたオブジェクトのセットからいくつの異なる配置を作成することができますか? | より大きなオブジェクトのグループからいくつの異なるグループを選択できますか? |
| 導出 | 単一の組み合わせからの多重置換 | 単一の順列からの単一の組み合わせ。 |
順列の定義
順列は、集合の一部またはすべてのメンバーを特定の順序で配置するさまざまな方法として定義されます。 それは、識別可能な順序に、与えられたセットのすべての可能な配置または再配置を意味します。
たとえば、文字x、y、zで作成されたすべての可能な順列 -
- 一度に3つすべてを取ることによってxyz、xzy、yxz、yzx、zxy、zyxです。
- 2つずつ取ることによってxy、xz、yx、yz、zx、zyです。
一度にr個取られるn個のものの可能な順列の総数は以下のように計算することができます。
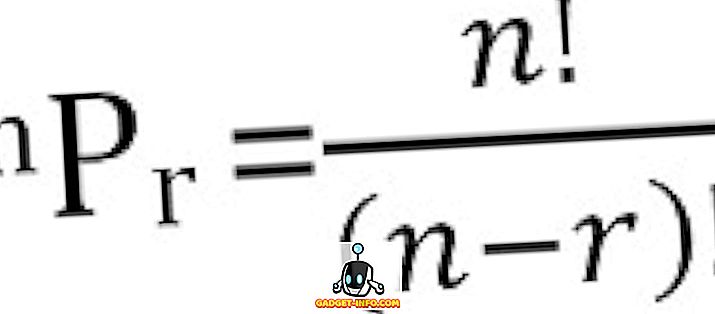
組み合わせの定義
組み合わせは、次の順序なしで、セットの一部または全部のメンバーを使用してグループを選択するさまざまな方法として定義されます。
例えば、文字m、n、oで選択されたすべての可能な組み合わせ -
- 3文字のうち3文字を選択する場合、唯一の組み合わせはmnoです。
- 3文字のうち2文字を選択する場合は、可能な組み合わせはmn、no、omです。
一度にr個取られるn個のものの可能な組み合わせの総数は次のように計算することができます。
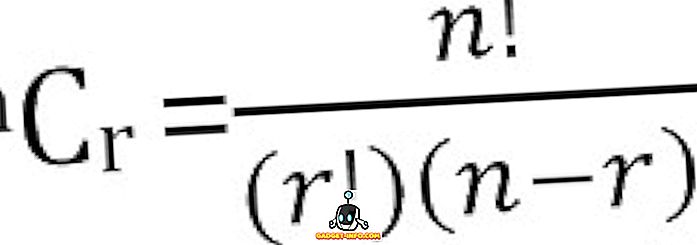
順列と組み合わせの主な違い
順列と組み合わせの違いは、以下の理由で明確に描かれています。
- 順列という用語は、一連のオブジェクトを順番に並べるいくつかの方法を意味します。 組み合わせは、オブジェクトの大きなプールからアイテムを選択するいくつかの方法を意味します。そのため、それらの順序は関係ありません。
- これら2つの数学的概念の間の主な区別点は順序、配置、および位置であり、すなわち上記の順列特性において重要であり、組み合わせの場合には重要ではない。
- 順列は、物、人、数字、アルファベット、色などを並べ替えるためのいくつかの方法を示します。一方、組み合わせは、メニュー項目、食べ物、服、主題などを選択するさまざまな方法を示します。
- 順列は順序付けられた組み合わせに他なりませんが、組み合わせは順序付けられていないセットまたは特定の基準内の値のペアリングを意味します。
- 多くの順列は、単一の組み合わせから導き出すことができます。 逆に言えば、単一の組み合わせからは単一の組み合わせしか得られない。
- 順列の答え与えられたオブジェクトの集合からいくつの異なるアレンジメントを作成することができますか? より大きなオブジェクトのグループからいくつの異なるグループを選ぶことができるかを説明する組み合わせとは対照的に?
例
3つのオブジェクトA、B、Cのうち2つのサンプルの合計サンプル数を調べなければならない状況があるとします。この質問では、まず最初に、質問が順列に関連しているかどうかを理解する必要があります。これを見つける唯一の方法は、順序が重要かどうかを確認することです。
順序が重要な場合、質問は順列に関連しており、可能なサンプルはAB、BA、BC、CB、AC、CAになります。 ここで、ABはBAとは異なり、BCはCBとは異なり、ACはCAとは異なります。
順序が無関係の場合、質問は組み合わせに関連し、可能なサンプルはAB、BC、およびCAになります。
結論
上記の説明で、並べ替えと組み合わせは異なる用語であり、数学、統計、研究、そして私たちの日々の生活において使用されていることは明らかです。 覚えておくべき点は、これら2つの概念に関して、与えられたオブジェクトのセットに対して、置換は常にその組み合わせよりも高いということです。