中心的傾向の理想的な尺度は、明確に定義され、容易に理解され、単純に計算可能なものです。 それはすべての観測に基づいており、データセットに存在する極端な観測による影響が最も少ないはずです。
人々はしばしばこれら2つの方法を対比しますが、事実はそれらが異なるということです。 この記事では、平均値と中央値の基本的な違いについて詳しく説明します。 見てください。
比較表
| 比較基準 | 平均 | 中央値 |
|---|---|---|
| 意味 | 平均とは、与えられた値または量のセットの単純平均を意味します。 | 中央値は、順序付けられた値の一覧の中央の数として定義されます。 |
| それは何ですか? | 算術平均です。 | 位置平均です。 |
| を表す | データセットの重心 | データセットの重心 データセットの中間点 |
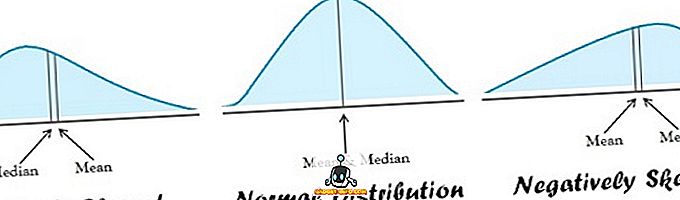
| 適用範囲 | 正規分布 | 偏った分布 |
| 外れ値 | 平均は外れ値に敏感です。 | 中央値は外れ値に敏感ではありません。 |
| 計算 | 平均値は、すべての観測値を合計してから、得られた値を観測値の数で除算することによって計算されます。 | 中央値を計算するには、データセットを昇順または降順に並べます。その場合、新しいデータセットの正確な中央にある値が中央値になります。 |
平均値の定義
平均は、中心的傾向の広く使用されている尺度であり、一連の値の平均として定義されます。 それはモデルと与えられた値の範囲の最も一般的な値を表します。 離散系と連続系の両方で計算できます。
平均は、すべての観測値の合計をデータセット内の観測値の数で割ったものに等しくなります。 変数によって想定される値が等しい場合、その平均も同じになります。 平均値は、標本平均値(x - )と母集団平均値(µ)の2種類があります。 それは与えられた式で計算することができます:
- 算術演算の意味

n =値の数 - ディスクリートシリーズの場合 :

- 連続サービスの場合

A =想定平均
C =公約数
中央値の定義
中央値は、中心傾向のもう1つの重要な尺度であり、値を2つの等しい部分、すなわち、サンプルの大半、母集団、または下半分からの確率分布に分割するために使用されます。 これは、観測値が昇順または降順の特定の順序でソートされたときに達成される、最も中間の値です。
中央値の計算では、まず最初に、観測値を最低から最高、または最高から最低に並べてから、以下の条件に従って適切な式を適用します。
- 観測数が奇数の場合

- 観測数 が 偶数の 場合

- 連続シリーズの場合 :

c =前の中央値クラスの累積度数
f =中央値クラスの頻度
h =クラス幅
平均値と中央値の主な違い
平均値と中央値の間の重要な違いは、以下の記事に記載されています。
- 統計学では、平均は与えられた値や量のセットの単純平均として定義されます。 中央値は、値の順序付きリストの中央の数字であると言われています。
- 平均は算術平均ですが、中央値は位置平均です。本質的には、データセットの位置によって中央値が決まります。
- 平均値はデータセットの重心を概説し、中央値はデータセットの中央値を強調します。
- 平均値は正規分布データに適しています。 反対に、中央値はデータ分布が偏っているときに最適です。
- 平均値は中央値の場合ではない極値によって大きく影響されます。
- 平均値は、すべての観測値を合計してから、得られた値を観測値の数で除算することによって計算されます。 結果は平均です。 中央値とは対照的に、データセットは昇順または降順に配置されているため、新しいデータセットのちょうど中央にある値は中央値です。
例
与えられたデータセットの平均値と中央値を求めます。
58、26、65、34、78、44、96
解決策:平均値を計算するには、観測値の合計を観測値の数で除算する必要があります。

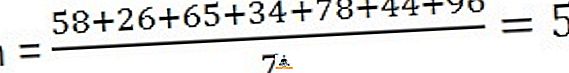
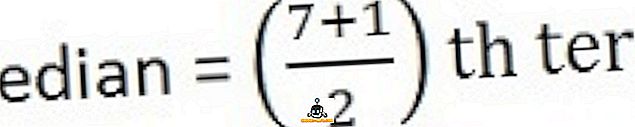
中央値を計算するには、まず最初に、系列を順番に、つまり最低から最高まで並べます。
26、34、44、58、65、78、96
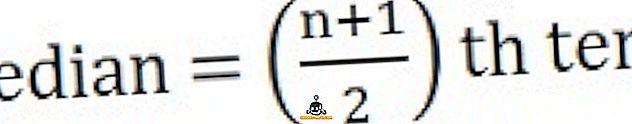
結論
上記の点を検討すると、これら2つの数学的概念は異なると言えます。 算術平均または平均は、理想的な尺度のすべての特徴を含むため、中心傾向の最良の尺度と見なされますが、サンプリングの変動が平均に影響を与えるという欠点が1つあります。
同様に、中央値も明確に定義されており、理解および計算が容易であり、この尺度の最大の利点はサンプリング変動の影響を受けないことですが、中央値の唯一の欠点はそれがすべてに基づいていないことです。観察 オープンエンド分類では、平均値よりも中央値が通常優先されます。