分類と回帰の違い

• 2019

分類と回帰は、通常データマイニングで扱われる2つの主要な予測問題です。 予測モデリングは、新しいデータを予測するために履歴データを使用してモデルまたは機能を開発する手法です。 分類と回帰の大きな違いは、分類によって入力データオブジェクトがいくつかの離散ラベルにマッピングされることです。 一方、回帰は入力データオブジェクトを連続実数値にマッピングします。

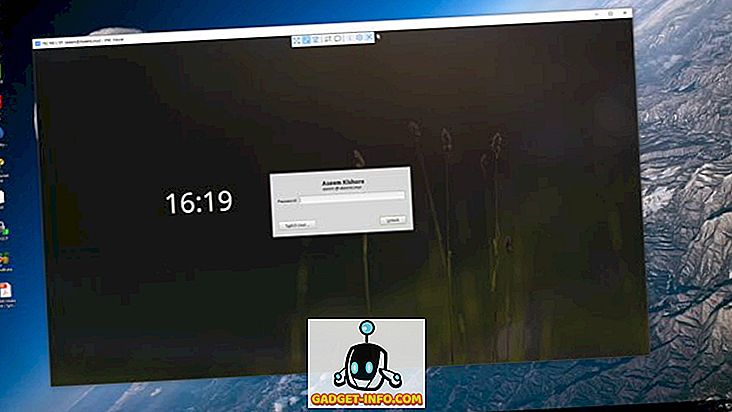
比較表

比較基準	分類	回帰
基本	オブジェクトのマッピングが事前定義されたクラスに行われるモデルまたは機能の発見。	オブジェクトのマッピングが値にされる工夫されたモデル。
の予測を含みます	離散値	連続値
アルゴリズム	決定木、ロジスティック回帰など	回帰木（ランダムフォレスト）、線形回帰など
予測データの性質	順不同	順序付けられました
計算方法	測定精度	二乗平均平方根誤差の測定

分類の定義

分類とは、データを複数のカテゴリクラスに分類するのに役立つモデル（関数）を見つける、または発見するプロセスです。 分類では、問題のグループメンバーシップが識別されます。これは、データがいくつかのパラメータに従って異なるラベルの下に分類されてからラベルがデータに対して予測されることを意味します。

導出モデルは、「ＩＦ − ＴＨＥＮ」規則、決定木またはニューラルネットワークなどの形で示すことができる。 決定木は基本的に、各内部ノードが属性についてのテストを表す木構造に似たフローチャートである。そしてその枝はテストの結果を示しています。 分類プロセスでは、データを2つ以上の離散ラベル、つまり2つ以上の互いに素なセットに分割できるという問題に対処します。

いくつかのパラメータに基づいて、ある地域で雨が降る可能性を予測したいとします。 それから、2つのラベルrainがあり、雨が降らないで、その下で異なる地域を分類することができます。

回帰の定義

回帰は、クラスを使用するのではなく、データを連続的な実数値に区別するためのモデルまたは関数を見つけるプロセスです。 数学的には、回帰問題で、最小の誤差偏差で関数近似を見つけようとしています。 回帰では、データの数値依存関係はそれを区別するために予測されます。

回帰分析は、ラベルの代わりに数値データを予測するために使用される統計モデルです。 利用可能なデータまたは履歴データに応じて流通の動きを識別することもできます。

いくつかのパラメータを使用して、特定の地域で雨が降る可能性があるという回帰分析でも同様の例を見てみましょう。 この場合、雨に関連する可能性があります。 ここでは、雨の中の地域や雨のラベルを分類しているのではなく、それらを関連する確率で分類しています。

分類と回帰の主な違い

1. 分類プロセスでは、離散クラスラベルでデータを予測するための関数をモデル化します。 一方、回帰は連続量を予測するモデルを作成するプロセスです。
2. 分類アルゴリズムは、決定木、ロジスティック回帰などを含む。対照的に、回帰木（例えばランダムフォレスト）および線形回帰は回帰アルゴリズムの例である。
3. 分類は順序付けられていないデータを予測し、回帰は順序付けられたデータを予測します。
4. 回帰は、二乗平均平方根誤差を使用して評価できます。 それどころか、分類は精度を測定することによって評価される。

結論

分類技術は、履歴データの助けを借りて離散的なカテゴリまたはラベルで新しいデータを予測する予測モデルまたは機能を提供します。 逆に、回帰法は連続値関数をモデル化します。つまり、連続数値データでデータを予測します。