標準偏差とは異なり、分散の計算中に得られた数値の平方根です。 多くの人がこれら二つの数学的概念を対比しています。 そのため、この記事では、分散と標準偏差の間の重要な違いについて説明します。
比較表
| 比較基準 | 分散 | 標準偏差 |
|---|---|---|
| 意味 | 分散は、その算術平均からの観測値の変動性を表す数値です。 | 標準偏差は、データセット内の観測値の分散の尺度です。 |
| それは何ですか? | それは偏差の二乗の平均です。 | それは二乗平均平方根偏差です。 |
| とラベルされた | シグマ2乗(σ^ 2) | シグマ(σ) |
| で表現された | 平方単位 | データセット内の値と同じ単位。 |
| を示します | グループ内の個人がどれだけ離れているか。 | データセットの観測値がその平均とどれほど異なるか。 |
差異の定義
統計学では、分散は、グループのメンバーがどれだけ分散しているかを表す変動の尺度として定義されます。 各観測値が平均値と異なる平均度数を求めます。 データセットの分散が小さい場合は、データポイントが平均に近いことを示しますが、分散の値が大きいほど、観測値は算術平均の周囲および周囲から非常に分散していることを表します。
未分類データの場合 :
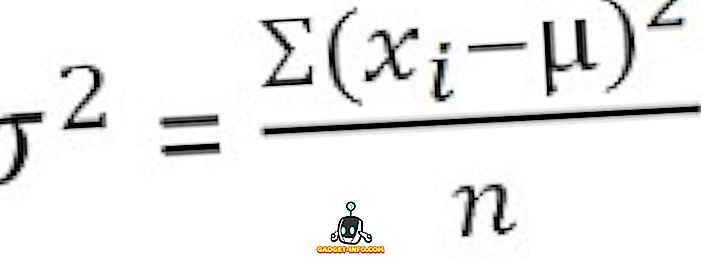
グループ化された頻度分布の場合
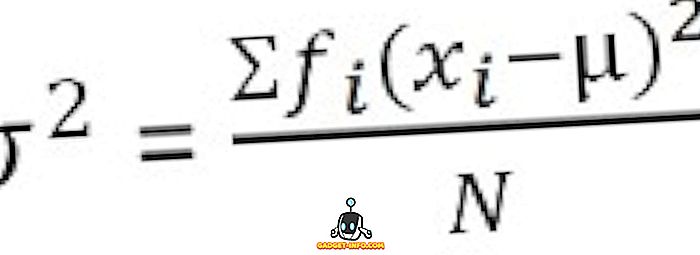
標準偏差の定義
標準偏差は、データセット内の観測値の分散量を定量化する尺度です。 低い標準偏差は、算術平均に対するスコアの近さの指標であり、高い標準偏差はを表します。 スコアはより広い範囲の値に分散されます。
未分類データの場合 :

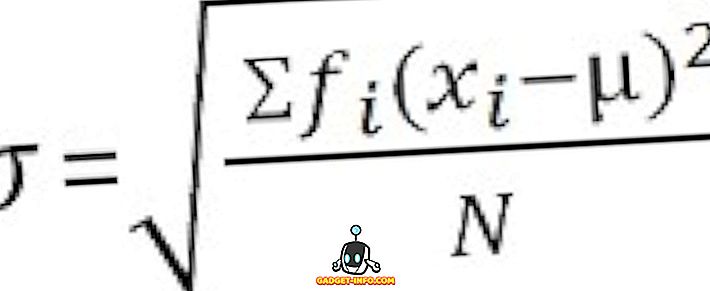
差異と標準偏差の主な違い
標準偏差と分散の違いは、次の理由で明確に説明できます。
- 分散は、その算術平均からの観測値の変動性を表す数値です。 標準偏差は、データセット内の観測値の分散の尺度です。
- 分散は二乗偏差の平均に他なりません。 一方、標準偏差は二乗平均平方根偏差です。
- 分散はシグマ二乗(σ2)で表され、標準偏差はシグマ(σ)として表示されます。
- 分散は、与えられたデータセットの値よりも通常大きい正方形の単位で表されます。 データセットの値と同じ単位で表される標準偏差とは対照的です。
- 分散は、グループ内の個人がどれだけ分散しているかを測定します。 逆に、標準偏差は、データセットの観測値がその平均値からどれだけ異なるかを測定します。
図
5つの科目で生徒が採点した点数は、それぞれ60、75、46、58、80です。 標準偏差と分散を見つけなければなりません。
まず最初に、あなたはその平均を見つけなければなりません、

そのため、平均(平均)マークは63.8です。
今度は分散を計算します
| バツ | A | (xA) | (XA)^ 2 |
|---|---|---|---|
| 60 | 63.8 | -3.8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316.84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262.44 |
ここで、X = Observations
A =算術平均
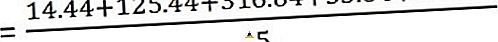
そして標準偏差は -

類似点
- 分散と標準偏差の両方が常に正です。
- データセット内のすべての観測値が同一の場合、標準偏差と分散はゼロになります。
結論
これら2つは基本的な統計用語で、さまざまな分野で重要な役割を果たしています。 標準偏差は測定値と同じ単位で表されるので平均よりも好ましいが、分散は与えられたデータセットより大きい単位で表される。